РАСЧЕТ СИСТЕМ ТЕЛЕУПРАВЛЕНИЯ В ЗАДАННОЙ СТРУКТУРЕ

Рассмотрим пример конкретного проектирования си­стемы телеуправления при заданной структуре ее конту­ра, считая его стационарным до точки встречи.

4.1. УЧЕТ ДИСКРЕТНОСТИ ПОСТУПЛЕНИЯ

ИНФОРМАЦИИ И ТЕМПА ВЫДАЧИ КОМАНД

Одной из основных особенностей систем телеуправле­ния является дискретность информации и управляющих объектом наведения команд [18]. Дискретность системы управления приводит к специфическим особенностям расчета контуров наведения [21]. Дискретный характер получаемой информации вносит дополнительные запаз­дывания в контур управления, повышает уровень спек­тральной плотности случайных ошибок измерения коор­динат, что приводит к снижению динамических качеств системы [24, 27, 28].

Рассмотрим упрощенную структурную схему контура наведения объекта в одной плоскости (рис. 4.1).

При теленаведении объекта до точки встречи имеем H(s) — 1. Если же этап теленаведения не является ко­нечным, то

Н (s’* =^„5 — f- 1,

где to— некоторое конечное время.

Определим характеристики оптимальной системы для стационарного случая, считая его основным в системах телеуправления, используя в качестве критерия опти­мальности «min Дел» при ограничениях на динамическую точность системы и дисперсию случайного ускорения «/ сл». т. е. рассмотрим задачу, аналогичную задаче, рас­смотренной в разделах 3.5 и 3.6 ддя непрерывной систе­мы.

ПреДПОЛОЖИМ, ЧТО Ti=T2=t3.

Функционал, подлежащий минимизации, имеет вид

/(«)=flL + tt7L+2Y/ft» С4;1)

/-0

где w — искомая весовая функция,

Рис. 4.1. Структурная схема контура телеуправления: Ть т2, т3 — ключи, соответствующие темпу измерения коор­динат цели Хц, объекта хр, передачи команд X; k*(z) — цифровое устройство выработки управляющей команды; ЗУ — запоминающее команду устройство на борту объекта; CDa(s) —контур стабилизации объекта с выходной коорди­натой ускорением /р; Фк($)—кинематическое звено; Пц(0> пр(0—ошибки измерения координат цели и объекта. Измерители координат на структурной схеме от­сутствуют. H(s)—оператор определения пролета системы

Определим дисперсии случайного пролета и ускоре­ния объекта

ОО 00

/в—оо — £ *=—оо

~2 2 *(‘-ж*)2®^-7+/т^л*-от]+

Е——оо /=- О

+ 2 w V ~7+/Т) 2 “*+$*){Я«[(5 —04 +

/-о е-0

+^Л(5-0т]}, (4.2)

где Rm, Rn — корреляционные функции соответственно случайных составляющих полезного сиг­нала и приведенной к единому входу по­мехи;

Nx— время памяти системы: і=в т;

0, I, I — целые числа;

— весовая функция идеальной системы.

Считаем, что весовая функция по ускорению объек­та для системы с теленаведением до точки встречи мо­жет быть определена как вторая разность, а для систе­мы с наведением до to— как первая разность весовой функции всей системы. Соответственно получим:

7L. T=2 “ *+/т) 2 д2да* (*~ЖТ)Х

/-о £-о

(4.3)

1

(*к — О2

(4.4)

при tK—t=t0 = const (fK— время наведения).

Суммируя выражения (4.3) и (4.4) по частям, по­лучим

Лл. т =2®т(* — tJrlx)’2i — ^+?т)Х

/=О £-0

X {д4/?т [(5-1) X]4- Д[(6 -1) t]}; (4.5)

х {д2/?т[(5-/)Л+д^я[(^-^)^> j

при граничных условиях

wT[t — О] =0; wT[t—t, (iV-fl)T] =0; д®т [t —t, О] =0; Ддат [t —t, {N-f 1) т] =0.

w0 [t—t, 0] =0; w0[t—t, (N + 1)t] —0. .

Условия (4.6а) аналогичны условиям (3.122) и (3.108).

Требование обеспечения заданной динамической точ­ности в установившемся состоянии может быть выполне­но как и в непрерывном случае с помощью моментных условий

2(ЛУ«(*-* + /т) = |1,. (4.7)

У-о

Подставляя выражения (4.2), (4.5), а также (4.6), (4.6а) и (4.7) в функционал (4.1) и минимизируя полу­ченные выражения, определим соответственно алгебраи­ческие уравнения относительно искомых w (t—t + k) для объекта, этап телеуправления которого заканчивается соответственно в точке встречи или в момент to.

N

т)

£-0

— V [(S — /) х + (|—/) г] Ц

ат I

2 ^^(кУ; (4.8)

—00 Z /-0

2®.(/-/+5т)|[>?я(5-/)т + /?(|(5-/)х]-

О-[ДвЯ«(«-0*+Лв/?.(?-/) t]) =

оао J

Е-—оо

(4.9)

і-О

где у, а — неопределенные множители Лагранжа.

Остановимся на некоторых наиболее простых част­ных случаях решения (4.8) и (4.9).

Пусть Rm(l — I) =0, п(/т)—дискретный «белый шум».

Тогда уравнения (4.8) и (4.9) обращаются в разно-, стные вида

Д4®», (t — tlx) —■ a4®rT {t—і+lx) =

= —ат[YoYx^T• • • +Ул(^т)л]ї (4.10) Д2®0 (t—?+lx) — а2 (t0f w0{t—f+ lx) =

= -<W[Yo+YA+. • . +Y. m (4.11)

откуда

Щ V~ t+ lx) = Ee%nt + Fe~%m+C sin S«t +

“ЬF) cos tix-f-Yo“b • • • +Уг(лт)‘! (4.12)

®o(/-?+ +Ве-*п’+% +

+ • • • +Y*(«t)’. (4.13)

Неизвестные константы E, F, C, D, А, В, у могут быть определены из граничных и моментных условий

®>т [t —і, о] =0;

wT[t — 1, (JV+l)t]=0; дw^{t—t, 0]=0;

д®т [t—t, (iV + l)t]=0; } (4.12,а)

*+ЛТ]=р0.

л-0

®0t-~t, 0] =0;

®0 t—t% (ЛГ + 1)т]=0;

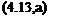N

2®o[^-^ + «t]=|i0

л-0

ПО

Параметры g и р, определяющие степень ограничения^ перегрузки объекта, аналитически выразить практически невозможно. Вычислить дисперсию перегрузки Дри фик­сированных значениях g или р достаточно просто. По­этому I и р целесообразно определять графически.

Для примера определим параметры весовой функции (4.13) в простейших случаях.

I случай.

Пусть

Xn{t) :«о-

Тогда

да0(г‘-/+лт)=Д^лх+Де-р/"4-у;. (4.14)

да0 [/ —І, 0] =0; w0[t-l, (7V + 1)t]=0;

N ‘

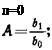/+Я»] = 1,

1 [sh ЗЛГт+sh —sh S (JV-f-1) tch ftf] 1 — ch p-r

—2((V + l)shp(W+l)t;

^! = 1 — ^—Р(лгн-і)х. b2=eP(iv+i)x_I; i,3=_2shp(TV-f 1)T.

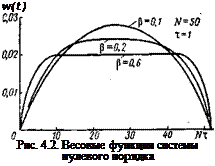
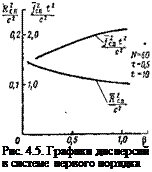
На рис. 4.2 изображены весовые функции (4.14) для условно принятых значений р, а на рис. 4.3 — графики дисперсий пролетов и ускорений объекта в зависимости от р.

Как следует из приведенных рисунков, при р—>-оо характеристики системы стремятся к характеристикам оптимальной системы без ограничений

R2

‘ сл (3->оо

с2 —дисперсия единичного замера координаты;

Ш

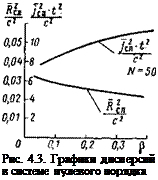дисперсия ускорения достигает максимального значе­ния, однако в отличие от непрерывной системы она не стремится в бесконечность вследствие ограничения спект­ра входного сигнала частотой квантования.

II случай.

Примем, что

(0 “ ^0

В этом случае

w{Xt-tArnx) = Ae^ +£eH5’"+Y*+Yi«T. (4.16)

Постоянные А, В, у*, Yi определяются из условий

®0 t — t, о] =0;

®0[*-F,(W + l)t]=0;

N

2®of<—■t—nr}= I;

п=0

N

2 nxw0t— ~t— nx= — —

n =0

Раскрывая 4.17, получим:

A — — •

bo ’

B=^-;

bo

*_ *3_.

Yo— h »

* .

Vi=r-;

0oT

N(N+ l)(N + 2) (—e~f(N+’)r і_еИлг+і)т 6 l—e~Pz —e? z }~ (ЛГ+1)[е~рт-ЛГе-Р

N+2

, я е-Р’_ЛГв-МЛГ+1)т(1__в-рт)_в-р(ЛГ+1)т ( + ^ (l_e-p-)2

+

ЛА(ЛА+1)е-?(лг+1)т I ( V I ^ l-e~P(jV+1)t

1 — e~Pz

^ АА(ЛА + 1)(АА + 2) І (Лг I іЛ N(2N+l)e*W+1>z 2 6 4 6

e? x-N(l — e? z)еР<лг+1)1:_ ePW+>)’

+

(1-е*

ИЗ

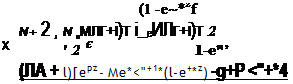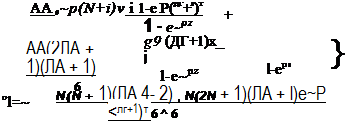е~Р* _ Ne~? (N+* )■* (I _ g-P*) _ e-P (ЛГ+1 )T (1 — e-^f

(l-ePx)2 *o + (V—|) Г N(N +1) _p (ЛН-1)

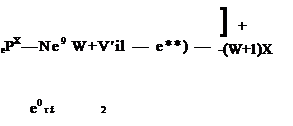N(2N+)e* (N+l)x

v, 1— е-Р(лг+1)т N(N+ 1) Лилг+1)т,

X TT7=^ 2 6 +

l_eP (V+1)T

l — e*[1]

eP,’_jVefl(;v’+,>T(l — g8t)_ e9(N+1)’

(1 — e^f

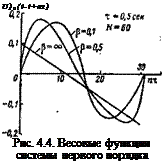
e-^ — Ne~* W+[2])’ (1 — e-^) — в-Р<лг+и*

X ( 1 — 0—P(W+t)T ) _ ^ + ]> -(g-P(JV+ly. _ e4N+1)TJ _

<0+ (/ — <) Г 1—в?(ЛГ+1)т f1 _P(AT+I)t4 n; [ 1_^ (1 * j

l_g Р(ЛГ + 1)т (W+l)^

При р = 0 получаем систему, оптимальную с точки зрения дисперсии перегрузки. Дисперсия пролета в этом случае возрастает ^ на 30~-40% [27].

;

Для дискретной системы второго порядка с ограниче­нием перегрузок решение принципиальных трудностей не представляет, однако является чрезвычайно громоздким и требует высокой точности вычислений. 4
вательного соединения дискретного F{tn) и непрерыв­ного F2(t) фильтров [31].

Будем искать, приближенную систему wn(t—t+nx) как последовательное соединение звеньев Fg(nx) и Fn{t) с неограниченным временем переходных процессов:

wn{t = Fн(* — — lx)Fg(lx). (4.19)

/-о

Учитывая, что оптимальная система является суммой произведений функций вида ф(/ — Ї) и ф(/т), предста­вим F* как

k

(t —1+ІХ — пх) = 2 <!>/ {і-— І) <? і (/т — пх), (4.20)

1=1

где k — число моментных и граничных условий на си­стему.

w(t-t+nx)

Рис. 4.6. Схема реализации весовой функции оп-
тимальной системы

Определяя неизвестные параметры Fn и Fg из момент­ных и граничных условий и подставляя их выражения в соотношение (4.19), можно получить весовую функцию приближенной системы.

Найдем выражение приближенной дискретно-непре­рывной системы на примере оптимальной системы пер­вого порядка. При этом для простоты опустим условие ограниченности перегрузок объекта, учет которого прин­ципиальных трудностей не вносит.

Тогда

(*■-І+ It) = Ы*~0 2 9i(lt-nx)Fg(пх) +

п =0

+м*-о2’,*(/’с—л*)/?*(лт)- (4-21)

Л-0

Приближенная система для обеспечения заданной динамической точности должна удовлетворять момент — ным условиям

00

Требуемое время переходного процесса и дисперсия пролета обеспечиваются обычно приближенно соответ­ствующим выбором свободного параметра системы.

Подставим выражение (4.21) в соотношения (4.22) и разрешим полученную систему уравнений относительно функций фі(£— t):

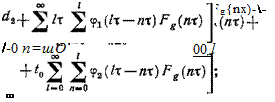Фа (^ — t),

li=Y 2 S?2 (/T ~ n%^Fg ^5

00 І

L — 2 /т 2 ?2 Vх — nx) Fe inx) X

Z=»0 ‘л=0

Х22?1^_/гТ^г(Л^-

г-о л-о

—21х 2?i (/т — йт) (wt)х Z-0 л-0

хІ2 <Ра(/т—ят) /^(лт); г-о п — о

Fa{t—t + lr—nx) =d(p (It—лт) +d2q>2{tx—nx) +
+ (f—г)[Афі (/т—лт) + k<p2 {h—лт)];

Fn(t—— пх)—^{1х — лт)+ (t—t)Lz{lx — nx). (4.27)

Так как функция Fn зависит от суммы аргументов (/ — Ї) и (1х — лт), она должна удовлетворять условию

dFH(t — t + lx — nx) __ dFH(t — f+lx — nx) 2g

d (t — ї) д (lx — nx)

Из условия (4.28) следует

L%=b; L1 — a-{-b{lx — nx),

т. е. FH(f—t—lx—nx)—a—b{t—t—lx — nx). (4.29)

Определив FH и подставив выражение (4.19) в соот­ношения (4.22), .найдем тождественные зависимости относительно аргумента (t—t)

а 22 ^ 22 (/т~ лт)^М +

/—О л-fО /“0 л—0

z=o л-о

л 2/т 2 Fe /т2 (lx ~пх>> Fe и)+

І —0 л —іО /—О л— О

+ь у — і) Jjlx 2 Fs (пхУ= -■*о — (*■- о*

г—о л—о

Условия (4.30) могут быть выполнены только в том случае, если дискретная система является дифференци­рующей второго порядка, т. е.

Fg{nx)=tfFgi{nx

при этом

Fg i(0)-0;

д/г, і(0)=0.

Требования (4.31) и (4.32) физически понятны, так как в рассматриваемом случае непрерывная система (4.29) имеет по! люс второго порядка, который необхо димо компенсировать.

Раскрывая выражения (4.30) и используя соотноше­ния (4.31) и (4.32), получим систему четырех алгебраи­ческих уравнений для определения параметров Fg(nx) и а, b системы при точном выполнении моментных усло­вий (4.22)

/V(0)=0; />,(т)=0;

(4.33)

2№С/?*1[(Я+1)Т]=Т”‘*’*

п~0

Зададим Fg(nx) в виде [см. (3.130)]

^г1(йт)=2^е_а’"Т — (4- 34)

г-1

Примем сц изменяющимися по геометрической про­грессии и из решения системы (4.33) определим дискрет­ную и непрерывную составляющие весовой функции при­ближенной системы.

Для системы первого порядка положим k — З, тогда

Fgl(tix)=A1e агп—А^е ^nz—A9e 4алт; 1 (4.35)

FH{t)=a—bt I

(е+2«_1)(е4ат_1) _

1 Ьт*(е3лх-)глх ’

g«x(g^_l)(e4«x_i) ^ _

3 г. т2(е3ат—і) ’ g

Ь’т {e~2az (е“*Т + і)(е2вт + і) (ват + 1)2 + ^

Й== (Є4яТ-і)(Є-2" + Є-« + і)

+ (в2ят + l)(e-2ctt + Є—1 + 1) [-7 (е2ат — 1)- e“Tjj

і ■ .

Параметр b перераспределяет коэффициент усиления между дискретной и непрерывной частями системы и мо­жет быть задан произвольно.

15 — 2

Выбрав а в виде а —1—, (4.37)

Nr

получим приближенную систему, дисперсия пролета ко­торой несущественно отличается от дисперсии оптималь-

ной системы, а время переходного процесса близко к рас­четному. Определим теперь выражения корректирующих устройств.

Представим структурную схему w(t — 7+пт) в виде рис. 4.7.

При телеуправлении до точки встречи имеем H(s) = 1.

ное соединение кинематического звена и бортового контура объекта Фв($).

Дискретное корректирующее звено К* (г) определяет­ся зависимостью

где z — символ 2-преобразования.
В рассмотренном примере

®«(*)

/С(г)=~ !°г2 + Нг, 22 + rf^ + rf2

где

/0 = Лі (g-5« — j-e-3»*) -(- Л2 (е~3«

11=-10е <0

<*,=-{(г-*"+е-!"+е-’+е’ £) +
"Мо [(^о — а/ 1 — е °) — 1J — 2}

Следует отметить, что заданная часть каждой си­стемы наведения для фиксирования команд, поступаю­щих на объект, должна содержать запоминающее уст­ройство с передаточной функцией

^з,(3)=—• (4.41)

Выражение (4.41) должно быть учтено при реализа­ции дискретной и непрерывной частей системы. Непрерыв­ная составляющая корректирующего устройства Фа (s)
может быть реализована соответствующим выбором стабилизирующих обратных связей при формировании автономного контура объекта, установкой фильтров но цепи прямого сигнала и т. д.

В качестве примера на рис. 4.8 приведены частотные характеристики некоторой приближенной системы, ап­проксимирующей рассмотренную оптимальную систему первого порядка.

Как видно из рис. 4.8, для реализации требуемой точ­ности в каждый момент времени непрерывные звенья коррекции в значительной степени участвуют в формиро­вании основных свойств системы.

Если непрерывная часть системы фиксированная, на­пример, контур стабилизации объекта удовлетворяет требованиям самонаведения, которые более жесткие, заданная точность может быть реализована с помощью цифрового фильтра только в моменты времени, кратные периоду квантования. Если время «памяти» системы

Т

значительно превосходит период дискретности (~^20),

то точность в промежутках между съемами информации существенно не изменится.